Die Erde ist flach!

DIE ERDE IST FLACH! Das ist kein Scherz. Was ich damit sagen möchte: die Erde ist aller Voraussicht nach KEINE KUGEL.
Ich habe gestern ein kleines "Experiment" gemacht und mal vom Konstanzer Hafen aus flach über den Bodensee nach Bregenz geschaut. Und jetzt dürft Ihr raten ;-): Bregenz war KOMPLETT zu sehen. Sogar die Masten der Segelboote im Bregenzer Hafen. Auf die Entfernung habe ich die natürlich mit meinem 20 x 60 Fernglas (20-fache Vergrößerung) nicht mehr einzeln gesehen, sondern als Konglomerat. Jedenfalls sind sie aber kein Stück "hinter dem Horizont" verschwunden. Ich stand ca. 2 m oberhalb der Wasseroberfläche. Meine Augen befanden sich also maximal 4 m oberhalb des Wassers.

Zunächst ein Hinweis: Weitere Artikel zur flachen Erde gibt es im "Flache Erde-Blog".

Sehen wir uns mal an, was die vermutlich größte Lügnerorganisation der Welt namens NASA sagt (die angeblich auf dem Mond waren und massgeblich mit verantwortlich für das Klimamärchen sind):
Unter "Distance to the Horizon" https://pwg.gsfc.nasa.gov/stargaze/Shorizon.htm finden wir dort folgendes: Eine ganz tolle Formel, mit deren Hilfe man berechnen kann, wie weit man "flach über das Wasser" sehen kann, wenn man eine Sichthöhe von 2 m hat: Distanz bis zum Horizont in km = Wurzel aus Sichthöhe (in km) x 112,88 km. Mit dieser Formel kommt man dann auf eine angebliche Horizontlinie, die bei der Sicht über Wasser (oder einer anderen völlig flachen Ebene) bei GERADE EINMAL 5 km liegt (exakt 5,05 km). Zur Klarstellung: alles was "hinter", also UNTERHALB dieser Horizontlinie, liegt (der Horizont "fällt" angeblich "ab", da die Erde ja angeblich in jeder möglichen Richtung gekrümmt ist), kann nicht nur schlecht, sondern ÜBERHAUPT nicht mehr gesehen werden, es sei denn, es wäre selber wieder so hoch, dass wenigstens ein Teil von ihm über die Linie des sichtbaren Horizontes ragt. Bei 4 m Höhe ergäben sich entsprechend maximal 7,14 km.

Nun sollten wir uns also fragen, weshalb Hatice und ich dann gestern MEHR ALS 45 km weit relativ niedere Gebäude von deren Grund aus am Rand des Sees sehen konnten: http://www.luftlinie.org/Konstanz/bregenz
Dieser Wert ist eventuell sogar noch "zu kurz", weil ich mir fast sicher bin, dass die "ball earthers" (im Englischen gibt es das Schimpfwort "flat earthers" für Menschen, die angebliche "wissenschaftliche Beweise" leugnen oder auf andere Weise "von gestern" sind) die angebliche Erdkrümmung mit einberechnet haben.
Die Antwort auf meine Frage, weshalb man über den Bodensee völlig problemlos mehr als 45 km weit entfernte und nicht besonders hohe Objekte am Ostufer des Sees ebenso wie die Uferlinie selber sehen kann, obwohl Bregenz aufgrund der angeblichen Erdkrrümmung angeblich 166!! m "tiefer" als Konstanz liegt (dies wird sogar auf einer aufwendig gemachten Tafel im Stadtgarten Konstanz "offiziell" behauptet, die ich nachfolgend abbilde), ist:
Weil nur hoch wissenschaftlich gebildete NASA-Mitarbeiter und Astronauten die Erdkrümmung sehen können.

Tafel im "Stadtgarten Konstanz" mit Informationnen über den Bodensee und der Behauptung, dass man angeblich auf einen 166 m hohen Turm steigen müsse, um Bregenz von hier aus zu sehen - siehe nächste Ausschnittfotografie

Ausschnittfotografie der im vorigen Bild abgebildeten Tafel im Konstanzer "Stadtgarten". Die orangefarbene Hervorbebung stammt von mir.

Normale "flat earthers" sehen hingegen die Erde so, wie sie nun mal ist: abgesehen von ihren teilweise nicht unerheblichen Erhebungen als flache "Scheibe" (Wie scheiben-, also kreisförmig die Erde genau ist, müsste man jetzt mal eruieren. Aber keine Angst: Ihr fallt NICHT am Rand herunter. Für diese Sichtweise gibt es auch eine sehr schlüssige Erklärung):

Quelle: http://en.wikipedia.org/wiki/Flat_Earth#/media/File:Flat_earth.png

Beim STANDARD-Modell der flachen Erde ist die Erde ringsum von einem Eiswall umgeben, der auf der angeblich globusförmigen Erde als "Antarktis" bezeichnet wird...

WICHTIGER HINWEIS: Ich bin inzwischen der Ansicht, dass dieses STANDARD-MODELL der flachen Erde mindestens genauso falsch ist wie das heliozentrische Modell, von mir als heliozentrisches Unfug-Modell, HUM, bezeichnet. Meiner Ansicht nach IST die Erde flach. Das zugehörige Standard-Modell gibt jedoch die Realität dieser flachen Erde nicht ansatzweise wieder. Die Erde ist meiner Ansicht nach NICHT von einem geschlossenen Eiswall umgeben und sie ist schon gar keine isolierte Scheibe, die "irgendwie" irgendwo herum schwebt. Weitere Informationen dazu auf meinem Flache Erde-Blog.

Wenn ich Euch jetzt neugierig gemacht habe, empfehle ich Euch z. B. diese Website: http://www.atlanteanconspiracy.com

Dort werden in mehreren sehr gut gemachten Videos dann auch viele der Fragen jedenfalls theoretisch beantwortet, die Euch jetzt vermutlich durch den Kopf schwirren - hoffentlich jedenfalls ;-).
(Achtung! In sehr vielen dieser Videos ist ein massiver Logikfehler enthalten. Laut dieser Videos lässt sich die behauptete Erddrehung angeblich damit widerlegen, dass Flugzeuge auch auf quer zur Erddrehung liegenden Landebahnen problemlos landen können und bei Nord-Süd-Kursen die Erddrehung nicht durch diagonale Kurse kompensieren müssen - sowie weitere nicht zutreffende angeblich "nicht wegzudiskutierende" Widerlegungen in Verbindung mit Flugzeugen. Diese sind aber seitens des Autors dieser Videos ausgemachter Blödsinn. Während sich die behauptete Kugelform der Erde als solche durch Beobachtungen wie die hier von mir geschilderten sehr leicht widerlegen lässt, ist das mit der behaupteten Erddrehung schon wesentlich schwieriger. Gegebenenfalls werde ich dazu mal einen eigenen Artikel schreiben. Bis dahin heißt es wie bei allem: selber denken ;-). Der Autor war meiner Argumentation leider nicht mal ansatzweise zugänglich, sondern hat mich sofort aus dem von ihm geleiteten Forum eliminiert. Das bedeutet natürlich jetzt nicht, dass die Erde kugelförmig wäre, sondern nur, dass der Autor leider ebenso pseudo-wissenschaftlich vorgeht, wie er das den "ball earthers" unterstellt).

Übrigens: nachdem wir jetzt die gaaaanz tolle, hoch offizielle Formel zur Ermittlung der Sichtweite "bis zum Horizont" kennen, kann jeder von Euch, der in der Nähe eines Sees lebt, der mindestens 5,05 km lang (oder gerne auch breit) ist, meine Beobachtung kinderleicht selber überprüfen: wenn Ihr von einem Ufer aus am anderen Ufer sehr niedrige Objekte, z. B. Schilf, kleine Büsche oder auch die Uferlinie selber sehen könnt (über eine Entfernung von 5 km kann man das mit jedem Fernglas problemlos erkennen), dann wisst Ihr ziemlich sicher, dass Ihr leider, leider kein NASA-Mitarbeiter seid, noch vermutlich je einer werden könnt.

"Flat Earthers" und Menschen, die selber denken und nachforschen, stellen die dort mit Sicherheit nicht ein...
GRINS.

Ich zeige Euch hier noch ein Foto, das Hatice vom Konstanzer Hafen aus aufgenommen hat - durch einen Klick auf das Bild könnt Ihr es vergrößern.

Am linken Bildrand erkennt man die Schlosskirche Friedrichshafen.

Hier ein weiteres Bild der Schlosskirche Friedrichshafen, aufgenommen vom Hafen Konstanz aus am 19.07.2015 mit einem 1m-Teleobjektiv (500 mm Spiegel-Teleobjektiv plus 2-fach Telekonverter). Aufgrund des "crop factors" der Kamera würde dieses Objektiv an einer Kleinbildkamera einem Teleobjektiv mit 2m Brennweite entsprechen. Leider war es an diesem Tag sehr dunstig, so dass wir Bregenz nicht ebenfalls von Konstanz aus aufnehmen konnten. Durch Anklicken lässt sich auch dieses Bild vergrößern.

Das nächste Bild bringt den endgültigen Beweis, dass die Schlosskirche in voller Höhe vom Ufer des Stadtgartens beim Hafen Konstanz aus zu sehen ist. Kein Stückchen ist "abgeschnitten", wie es zu erwarten wäre, wenn die Kirche aufgrund einer eventuell vorhandenen Krümmung auch nur teilweise "unter den Horizont sinken" würde. Dieses Bild wurde am 18.08.2015 gegen 17:30 Uhr aufgenommen. Wie man sehen kann, war der Himmel komplett bewölkt. Auf der Hinfahrt regnete es leicht und auf der Rückfahrt stark. Eine eventuelle "Luftspiegelung" als Ursache der vollständigen Sichtbarkeit ist also allein aufgrund der Wetterbedingungen bereits ausgeschlossen.
Öffnet bitte das große Bild durch Anklicken des Übersichtsbildes und schaut Euch sehr genau die Strukturen an, von denen ich eine mit einem roten Pfeil markiert habe. Diese Strukturen sind, wie auf dem nächsten Bild sehr deutlich zu erkennen, Nadelbäume vor der Kirche, die wir bis auf den Grund sehen können. Weiterhin ist deutlich die graue Uferpromenade vor der Schlosskirche zu erkennen.

 

Zum Vergleich ein Luftbild der Schlosskirche aus dem Internet. Auch dieses Bild lässt sich durch Anklicken vergrößern. Sehr deutlich sind die Nadelbäume vor der Kirche zu erkennen.

Quelle dieses Bildes: Bitte hier klicken...

Die Entfernung zwischen Konstanz und der Schlosskirche Friedrichshafen beträgt ca. 21 km Luftlinie.

"Eigentlich" hätte aber der Horizont bereits nach 5 km "alles verschlucken" sollen. Und argumentiert jetzt bitte nicht, dass die Kirchtürme ja 55 m hoch seien.

ERSTENS würde der Erdboden bei einer tatsächlich runden Erde laut NASA-Formel nach 21 km bereits ca. 35 m "unter den Horizont fallen" (sogar 51 m unter Berücksichtigung der Tatsache, dass der Bodensee nicht am Äquator, sondern auf 47.6° nördlicher Breite liegt, auf der der "Erdradius" - streng genommen selbstverständlich der Radius des durch diesen Breitengrad definierten Kreissegments - mit nur noch angeblichen 4.296 km bereits wesentlich geringer als am Äquator wäre, wenn es denn einen Äquator auf einer Erdkugel gäbe - Erläuterung unten unter "Update III"; für die Kugelerde-Großkreis-Fanatiker habe ich dort ebenfalls einen entsprechenden Hinweis), so dass von den Kirchtürmen nur ca. MAXIMAL das obere Drittel (oder so gut wie nichts mehr bei Berücksichtigung des Breitengrades) zu sehen sein dürfte.
Die Fotografie vom 18.08.2015 zeigt aus meiner Sicht noch etwas sehr Interessantes und Schönes: bei genauer Betrachtung erkennen wir, dass die Rümpfe der drei Segelboote - teilweise - "abgeschnitten" zu sein scheinen. Dieser Effekt führt bei den Kugelerde-Gläubigen regelmässig zu Freudenausbrüchen, gilt dies doch als "Beweis" dafür, dass die Erde angeblich eine Kugel sei. Es gibt unzählige Videos im Internet, die genau diesen Effekt zeigen und dann mit Sprüchen wie "Flache Erde Ade" und dergleichen triumphieren. Gleichzeitig ist aber auf meiner Aufnahme eine merkwürdige "weiße Welle" zu sehen, die ganz eindeutig ALLEIN für das OPTISCHE Verschwinden der Bootsrümpfe UND dafür verantwortlich ist, dass OPTISCH ein kleiner Teil der Kaimauer vor der Schlosskirche "abgeschnitten" SCHEINT.
Ganz offensichtlich gibt es bestimmte Licht- und Wetterbedingungen, unter denen diese rein optischen Effekte auftreten (vermutlich spiegelt die Wasseroberfläche das Licht auf eine Weise, dass auf die große Entfernung dann Bootsrümpfe und ähnliches nicht mehr zu sehen sind), die zu der rein OPTISCHEN TÄUSCHUNG eines "Verschwindens" oder "Abschneidens" von Bootsrümpfen und ähnlichem führen. Siehe dazu auch hier!
Die Schlosskirche selber befindet sich außer- und oberhalb des Wassers und wird daher - bis auf einen kleinen Teil der Kaimauer - nicht von diesem rein optischen Phänomen betroffen.
Da sich die Schlosskirche in einem von jedermann nachprüfbaren, definierten Abstand vom Stadtgarten Konstanz, von dem aus die Aufnahme gemacht wurde, befindet und hier nur ein mininmaler, angesichts der 35 m, die "abgeschnitten" sein müsssten, ohnehin vollständig zu vernachlässigender Teil der Kaimauer OPTISCH DURCH die "weiße Welle" abgeschnitten wurde, kann diese Aufnahme gleichzeitig als Falsifizierung des - falschen - Arguments gelten, dass "verschwindende" oder "abgeschnittene" Bootsrümpfe die Kugelerde "beweisen" würden.

Zweitens ist auf ALLEN Fotografien, die Hatice und ich aufgenommen haben, sehr deutlich zu sehen, dass man die Türme in VOLLER HÖHE einschließlich der davor stehenden wesentlich niedrigeren Bäume und der Uferlinie sieht.

Irgendwie will das mit der runden Erde am Bodensee nicht so hinhauen...
Über die 4-fache Entfernung (5 km), die laut NASA angeblich möglich sein soll, war es uns mehrfach problemlos möglich, die Schlosskirche Friedrichshafen in voller Höhe zu sehen und fotografisch zu dokumentieren. Wenn die Erde eine Kugel wäre, müsste sie unter diesen Voraussetzungen SECHZEHNMAL so groß sein, wie behauptet wird (Erklärung dazu unten unter Update III).

Ich warte jetzt "eigentlich" drauf, dass mir jemand eine Theorie vorlegt, derzufolge der Bodensee "wissenschafltich bewiesen" eine ziemlich gewaltige Ausnahme von der allgemein üblichen und - laut NASA - überall gleichermassen sichtbaren Erdkrümmung macht. Aber wohlgemerkt NUR der See als solcher. Die Erde "darunter" und daneben und vorne und hinten ist selbstverständlich gekrümmt. Oder wer möchte gerne ein "Flat Earther" sein?

Ich!

Übrigens: es gibt Panorama-Aufnahmen vom Mount Everest aus dem Jahre 1989. Damals war die Erde auch schon flach ;-).

Hier weitere interessante Beobachtungen, die gar nicht so recht zum Kugelerde-Modell passen wollen: http://n8waechter.info/2016/07/nordsee-juli-2016-fotos-fragen-und-die-erkenntnis-hier-stimmt-was-nicht/

Das bekannte "Flache Erde"-Magazin "Mallorca Zeitung" (die natürlich tatsächlich mit "Flacher Erde" rein gar nichts zu tun hat), zeigt dieses interessante Bild, bei dem jemand aus "rund" 200 km Entfernung und aus 400 m Höhe die Serra de Tramuntana in Mallorca fotografiert hat, die laut Wikipedia eine MAXIMALE Höhe von 1.445 m über Meeresspiegel aufweist.
Ich höre meine "Kugelerde"-Fans, deren extrem ausgefeilte Argumentation ich inzwischen zur Genüge kenne, schon jubeln: Aus 400 m Höhe ist doch wohl klar, dass man das sehen kann.
Wirklich?
Rechnen wir kurz nach: Da ich keine Lust mehr habe, immer wieder Formeln nur deshalb herzuleiten, weil jemand "eine bessere kennt", nehme ich jetzt einfach die aus Wikipedia. Dort ist genau für diesen Fall, dass BEIDE Objekt über der Wasserlinie liegen, diese Formel hergeleitet, die sogar schon die angebliche "terrestrische Refraktion" - siehe weiter unten unter Update IV - berücksichtigt: s = 3,9 x (√h1 + √h2)
Für diese Formel sind h1 und h2 in Metern einzugeben und als Resultat werden km für s erhalten. Nachdem eine kurze Überprüfung bei luftlinie.org zeigt, dass exakt 200 km ein sehr guter Wert für den horizontalen Abstand beider Objekte ist, können wir nun mit der Betrachtung fortfahren. Die Entfernung, bei der man die Serra de Tramuntana überhaupt nicht mehr sähe, würde 226,25 km betragen. Jubel bei den "Kugel-Erdern".
Wirklich?
Nun brauchen wir doch wieder ein klein wenig Mathematik ;-):
Schritt 1:
s = 3,9 x (√h1 + √h2) ist gleichbedeutend mit:
Schritt 2:
s = 3,9 x √h1 + 3,9 x √ h2
Schritt 3:
(s - 3,9 x √h1) = 3,9 x √h2
Durch Quadrierung auf beiden Seiten erhalten wir:
Schritt 4:
(s - 3,9 x √h1)² = 15,21 x h2
Die Auflösung der binomischen Formel ersparen wir uns, weil der Bandwurm sonst zu lang wird...
Schritt 5: h2 = (s - 3,9 x √h1)² / 15,21

Damit ergibt sich h2 bei einer Entfernung von 200 km und einer Beobachterhöhe h1 von 400 m zu ca. 979 m. Das ist die Höhe, die NICHT MEHR sichtbar WÄRE. Dadurch bleiben von der Gipfelhöhe der Serra de Tramunata 466 m übrig. Nun sehen wir aber auf dem Bild deutlich den GESAMTEN Gebirgszug, der auch, wie deutlich zu erkennen, WESENTLICH niedrigere Gipfel enthält.
Ach ja, halt! NATÜRLICH ist das eine LUFTSPIEGELUNG. Ja, was denn sonst? Am, Zitat, "frühen Montagmorgen", gell? Wie man auf dem Bild sieht, wurde das ja bei gleissendem Sonnenschein, also optimalen Bedingungen für eine Luftspiegelung, aufgenommen ;-).

Auf github finden wir eine sehr schön aus dem Satz des Pythagoras hergeleitete Formel, die dort bedauerlicherweise nicht bis zu Ende ausformuliert ist, was ich hiermit hier nachhole:

Zunächst die dort verwendeten Definitionen:

h0 = Augenhöhe (oder Höhe einer Kameralinse)
h1 = Höhe des anvisierten, "hinter dem Horizont verschwundenen" Ziels, was der Höhe der "Erdkrümmung" an diesem Punkt entspricht.
d1 = Entfernung bis zum Horizont, also bis zu dem Punkt, an dem das Licht auf die "gewölbte" Wasserlinie trifft
d2= Entfernung vom Horizont bis zu h1
d0 = Gesamtentfernung Beobachter bis zum Ziel, also d0 = d1 + d2
R = Radius der "Erdkugel"

Aus dem Satz des Pythagoras ergibt sich dann: (R + h0)² = (d1)² + R²

--> (d1)² = (R + h0)² - R²

--> (d1)² = R² + 2Rh0 + (h0)² - R²

--> d1 = √((h0)² + 2Rh0) -- Gleichung 1

Für h1 ergibt sich ebenfalls: (R + h1)² = (d2)² + R²

--> R + h1 = √((d2)² + R²)

--> h1 = √((d2)² + R²) - R -- Gleichung 2

Ferner ist d2 = d0 - d1, woraus Gleichung 2 transformiert wird zu:

h1 = √((d0 - d1)² + R²) - R -- Gleichung 3

Ersetzen wir nun d1 aus Gleichung 1, ergibt sich:

Hierbei sind alle Werte in km einzusetzen und h1 ergibt sich folglich zu km.

Da es etwas mühselig ist, diesen Bandwurm auszurechnen, hat uns github freundlicherweise diesen Rechner zur Verfügung gestellt: https://dizzib.github.io/earth/curve-calc/?d0=46&h0=4&unit=metric, mit dem sich für die Situation für das Photo der Sera Tramuntana sogar eine "verschwundene" Höhe von 1.298 m, also eine "sichtbare" Höhe von maximal 147 m ergibt.

Unter diesem link sehen wir die Spitze des El Teide (Teneriffa), von El Costillo, Fuerteventura, aus aufgenommen: https://www.facebook.com/Arcatindaya/posts/1058721534178562?pnref=story Nach Aussage einer Bewohnerin von El Costillo, die mir den link sandte, gibt es dort maximal dreigeschossige Häuser. Die Luftlinie, über die dieses Foto aufgenommen wurde, beträgt mindestens 250 km. Die "Kugelerde" müsste auf diese Entfernung 4,9 km "abfallen". Der El Teide ist aber laut Wikipedia nur 3.718 m hoch.

Derselbe Fotograf hat noch ein anderes Bild aufgenommen: Gran Canaria, nach Aussage derselben Fuerteventuar-Bewohnerin, auch von El Costillo aus fotografiert.

Noch ein interessantes Video, das deutlich zeigt, dass der Horizont der Erde eine gerade Linie ist: https://www.youtube.com/watch?v=ZMceuZ6NoIM

Und noch ein Bild, das die Kugelerde-These sehr deutlich in Frage stellt: https://www.facebook.com/photo.php?fbid=795116297280779&set=gm.191618424513958&type=3 Nach Auskunft der Fotografin wurde der Mount McKinley aus einer Entfernung von 200 Meilen (ca. 322 km) fotografiert. Ich kann das nicht überprüfen, halte das Foto aber dennoch für interessant genug, es hier zu veröffentlichen.

Update 02.07.2024: Um die Beobachtungen zur Sichtbarkeit entfernter Objekte einordnen zu können, empfehle ich diesen Artikel von mir, der rund 9 Jahre nach meinen Beobachtungen am Bodensee entstanden ist.

Update: Wusst ich´s doch! Es gibt bereits eine erste Theorie, die meine Beobachtungen außerordentlich schlüssig erklärt und beweist, dass die Erde nur rund sein kann. Mensch, da hätte ich aber auch mal selber drauf kommen können: Die Erde ist selbstverständlich rund, aber dank einer LUFTSPIEGELUNG konnte ich alles ganz wunderbar sehen. Klar! Am 17.05.2015, bei ca. 22° C Aussentemperatur gegen 17 Uhr abends (okay, okay, in Wahrheit war es erst 16 Uhr wegen der Sommerzeit) und herrlich bayerischem weiß-blau bewölktem Himmel (huch: der Bodensee liegt ja gar nicht in Bayern ;-) - muss wohl an der Luftspiegelung liegen  (mich hat allerdings ein aufmerksamer Leser darauf hingewiesen, dass ein kleiner Teil des Sees von Nonnenhorn bis Lindau-Zech noch innerhalb Bayerns liegt) - UND darüber hinaus genügend Wind, dass der Bodensee von sehr vielen Segelbooten bevölkert war (Voraussetzung für eine Luftspiegelung ist u. a. Windstille; Segelboote siehe das abgebildete obere Foto mit der kleiner abgebildeten Schlosskirche), gibt es ausgerechnet über ganz Bregenz eine Luftspiegelung (wie viele solcher Luftspiegelungen haben wir in unseren Breitengraden noch mal im Schnitt pro Jahr? Und wo genau tauchen die immer auf?), die mir die Illusion vermittelt, dass Bregenz genau da wäre, wo es nun mal ist. Und deshalb konnte ich Bregenz auch nur mit dem Fernglas sehen. Das ist ja auch bei Luftspiegelungen immer so, gell? Bei jeder Fata Morgana sieht man ja immer die Stadt da, wo sie gerade ist UND man braucht unbedingt ein Fernglas, um sie zu sehen. Deshalb wissen die Menschen, wenn sie die Fata Morgana einer Oase sehen, auch ganz genau, dass da wirklich eine ist und freuen sich schon auf das kühle Nass. Deshalb wird eine Fata Morgana dann ja auch als Sinnestäuschung bezeichnet.

Darüber hinaus war die Luftspiegelung selbstverständlich nicht nur über Bregenz, sondern auch und erst recht über Friedrichshafen, also ca. um ein viertel des ganzen Bodensees präsent.

Wir waren übrigens inzwischen insgesamt dreimal an ganz unterschiedlichen Tagen in Konstanz am Bodensee. Bei unseren letzten beiden Besuchen konnten wir wegen starken DUNSTES Bregenz nicht sehen. Wir haben aber jedes einzelne Mal die Schlosskirche in Friedrichshafen entdeckt. Wenn mir jetzt noch jemand erklärt, dass es IMMER dann, wenn ich zum Bodensee fahre, eine Luftspiegelung gibt, die mich auch bei starkem Dunst diese Kirche inklusive des Dunstes sehen lässt, glaube ich dieser These der Luftspiegelung vielleicht irgendwann...

Update II: Meine Beobachtung entwickelt sich langsam zum Jahrmarkt der Abstrusitäten. Nach der Luftspiegelung wird es jetzt noch besser: Ich konnte Bregenz über eine Entfernung von mehr als 45 km sehen, weil das LICHT RELATIVISTISCH GEBEUGT WIRD. Ja HAMMER.
Ich tue es ja nicht gerne, aber in diesem Fall kontaktieren wir doch einfach mal Wikipedia. Dort lesen wir folgendes, wenn wir "Lichtkrümmung" eingeben: "Die Shapiro-Verzögerung, benannt nach Irwin I. Shapiro, lässt die Ausbreitung von Licht in der Nähe einer großen Masse für einen weit entfernten Beobachter langsamer als mit Lichtgeschwindigkeit erscheinen. Dies steht im Einklang mit der Allgemeinen Relativitätstheorie.
Der Gravitationslinseneffekt, bei dem Licht durch Gravitation abgelenkt wird, lässt sich mit der Shapiro-Verzögerung erklären. Dabei ergibt sich die Ablenkung ähnlich wie bei der Brechung von Licht an Linsen aus Glas, aus einer lokalen Änderung der Ausbreitungsgeschwindigkeit."

UND, GANZ WICHTIG: "Am Sonnenrand ist phi = 10^{-6} woraus sich als Brechungsindex n = 1,000002 ergibt. Der Effekt ist also im Vergleich zur gewöhnlichen optischen Brechung sehr klein. Dementsprechend klein ist auch der Winkel der Lichtablenkung im Gravitationsfeld."

Halten wir also fest: die angeblich RIESIGE Masse der Sonne (angeblich 1,99 Quadrilliarden Tonnen oder 332.946 Erdmassen laut Wikipedia) bricht das Licht angeblich auf eine Weise, dass es sich in der SECHSTEN Stelle nach dem Komma auswirken soll, aber der Bodensee, als winziger Teil von nur einer Erdmasse (sehr gerne aber auch die eine Erdmasse als ganzes), bricht das Licht dermassen, dass ich plötzlich 166 m "um die Kurve" sehen kann. Ganz abgesehen davon, dass eine Entfernung von 45 km ganz sicher nicht dem Kriterium "weit entfernter Beobachter" entspricht, bei der eine wie auch immer geartete "Verlangsamung" der Lichtgeschwindigkeit auch nur ansatzweise ins Gewicht fallen würde. Bei einer Lichtgeschwindigkeit von 300.000 km/s müssten unsere Sinnesorgane - Auge und Gehirn - schon wahrhaft übermenschliche Leistungen vollbringen, um auch nur entfernt an den Effekt einer möglichen Lichtkrümmung denken zu können.

Ich muss allerdings an dieser Stelle endlich mal ein Geheimnis presisgeben: Das Fernglas, das ich verwendet habe, ist ein ganz spezielles: Es erzeugt nicht nur an jeder beliebigen Stelle, bei jedem beliebigen Wetter und zu jeder Tages- und Nachtzeit spontane Luftspiegelungen. Es hat auch einen hoch effizienten relativistischen Lichtbeuger eingebaut, den ich ständig weiter entwickle. Leute, passt auf: bald bin ich so weit, dass ich das Licht 360° beugen kann. Das Patent werde ich dann an die NSA verkaufen. DANN geht´s aber los! Die können Euch ÜBERALL beobachten. Um jede noch so kleine Ecke schauen.

Update III: Immer wenn ich denke, es kann nicht noch absurder werden, werde ich vom Leben eines Besseren belehrt. Vor kurzem kam folgendes "Argument": Weil die Erde rund ist und weil jeder weiß, dass man auf dieser runden Erde sehr weit sehen kann, kann die von der NASA verwendete Formel nur falsch sein. Das ist mal richtig genial. Nach Karl Popper muss eine Theorie einer Falsifizierung widerstehen, wenn sie sich als richtig erweisen soll. Hier wird nun aber mit der Theorie als "Beweis" argumentiert, um das zu falsifizieren, also die Formel, was die Theorie (der runden Erde) im Zusammenhang mit für jeden leicht nachvollziehbaren Beobachtungen sofort falsifiziert.

Mir zeigt das allerdings, dass teilweise wohl einfach noch erweiterter Erklärungsbedarf besteht. Also machen wir uns auf, die von der NASA verwendete Formel, die übrigens nichts weiter als Mathematik der 9. Klasse Gymnasium verwendet, ganz sauber herzuleiten.

 

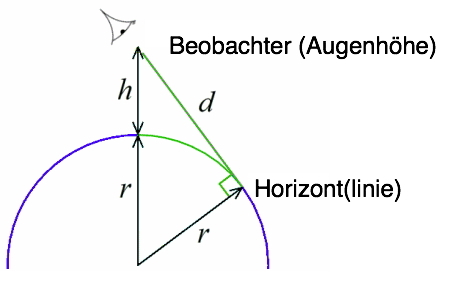
Wie wir sehen können, klärt die auch von der NASA verwendete Formel die Frage, wie weit man in Abhängigkeit von der Höhe seiner Augen oberhalb der Erdoberfläche auf einer kugelförmigen Erde sehen kann. Diese Frage lässt sich geometrisch lösen, indem eine TANGENTE vom höchsten Punkt des Beobachters (Augenhöhe) an den Kreis angelegt wird. Alles jenseits der Tangente kann nicht mehr gesehen werden, weil es aufgrund der Kugel - oder hier vereinfacht Kreisform als Schnitt durch eine Kugel  - UNTERHALB der Linie liegt, an der sich für das Auge/Gehirn der Horizont darstellt, an dem also sozusagen der Himmel mit der Erde (oder dem Wasser) optisch verschmilzt.
Wie wir sehen, ist der einzige und wesentliche Parameter der gesamten Formel der RADIUS des Kreises oder, in unserem Fall, der Erde. Die Linie "d" ist die Distanz bis zum Horizont, die wir wissen möchten. Sie beeinflusst also das Ergebnis überhaupt nicht, da sie der GESUCHTE Parameter ist. Die Höhe "h" beeinflusst selbstverständlich das Ergebnis, aber sie ist VORGEGEBEN und somit variabel. Damit bleibt "r" als einziger relevanter Parameter übrig.
Wie wir weiter sehen, bildet die Linie "r" am Punkt der Horizontlinie mit der Linie "d" einen rechten Winkel. Das ist übrigens unabhängig von der Höhe "h" immer so, da das Wort "Tangente" mit der Winkelfunktion "Tangens" nicht zufällig verwandt ist. Die Winkelfunktionnen sind im rechtwinkligen Dreieck gültig; gleichzeitig handelt es sich bei diesen aber um Kreisfunktionen. Siehe z. B. https://de.wikipedia.org/wiki/Tangens_und_Kotangens

Wie allgemein bekannt ist, lässt sich für rechtwinklige Dreiecke der Satz des Pythagoras anwenden (c² = a² + b²). Die Strecke, die sich aus "r + h" bildet, ist die Hypotenuse, c, des rechtwinkligen Dreiecks.
Diese Formel ist also nichts weiter als die mathematische Umsetzung der geometrischen Gegebenheiten einer kugelförmigen Erde, so sie denn so aussähe.

Damit gilt: (r + h)² = r² + d².

Wir wenden die 1. Binomische Formel an und erhalten:
SCHRITT 1: r² + 2rh + h² = r² + d²

Wir subtrahieren auf beiden Seiten r² und erhalten:
SCHRITT 2: 2rh + h² = d²

Wir klammern auf der linken Seite h aus und erhalten:
SCHRITT 3: h(2r + h) = d²

Nun ergibt sich allerdings ein Problem, denn diese Formel lässt sich nicht weiter "auflösen". Allerdings lässt sie sich unter Akzeptanz einer naheliegenden Annahme so vereinfachen, dass sie lösbar wird und näherungsweise richtige Ergebnisse liefert: das rote "h" innerhalb der Klammer ist im Vergleich zu 2r so klein (r repräsentiert ja den Radius der angeblichen Erdkugel), dass es vernachlässigbar wird und damit einfach weggelassen werden kann. Bekanntermassen wird der Erdradius, um den es sich in unserem Fall bei "r" handelt, mit im Mittel 6.371 km angegeben: https://de.wikipedia.org/wiki/Erdradius
2r, also der Durchmesser der angeblichen Erdkugel, würde dann 12.742 km betragen.
Selbst wenn ein Beobachter auf 100 km aufstiege, wäre der Fehler, der sich durch Weglassen des roten "h" ergibt, also immer noch kleiner 1% (100 / (100 + 12.742) = 0,78%).

Unter dieser Annahme, also unter Weglassen des roten "h" in der Klammer, erhalten wir dann folglich:

SCHRITT 4: h x 2r = d²

Unter "Wurzelziehen" ergibt sich dann:

SCHRITT 5: d = √h x √2r

Wir setzen für "r" den oben angegebenen angeblichen Erdradius von 6.371 km ein und erhalten:

SCHRITT 6: d = √(2 x 6.371km) x √h = 112,88 km x √h (km).

Auf genau dieselbe Formel kommt auch die NASA in dem weiter oben angegebenen link:

Laut NASA: D = 112,88 km x √h (km)

Und wenn wir in diese Formel eine Augenhöhe von 2 m einsetzen (was für den Durchschnittsmenschen sogar noch zu viel ist), kommen wir auf eine "Entfernung bis zum Horizont", jenseits derer dann alles "unter die Horizontlinie" fällt, von gerade einmal 5,05 km.

Dieser Wert ist aber aus einem anderen Grund noch viel zu optimistisch: bekanntlich leben wir in Deutschland nördlich des 47. Breitengrades. Der Breitengrad für den Bodensee wird mit 47,6° nördlicher Breite angegeben.
Unter https://de.wikipedia.org/wiki/Geographische_Breite finden wir die Abhängigkeit der Abnahme des Radius des Kreissegments einer Kugel von dessen "geographischer Breite":

r_B = r x cos B, wobei:

r_B: Radius des Breitengrades

r: Radius am Äquator (0° Breite)

B: Breitengrad

Daraus ergibt sich für 47,6° nördlicher Breite ein Radius des Kreissegments von nur noch 4.296 km (0,67 x 6.371 km).

Wenn wir diesen Radius nun in die obige Formel, SCHRITT 6, einsetzen, kommen wir sogar nur noch auf eine "Sichtweite bis zum Horizont" von 4,15 km (für den Fall, dass wir "entlang des Breitengrades", also in ost-westlicher Richtung blicken).

An dieser Stelle ein ernst gemeinter Hinweis an die Kugelerde-Großkreis-Fanatiker: ich kenne selbstverständlich die - angesichts der Größe der angeblichen Erdkugel völlig absurde - Argumentation, dass man auf einer Kugel, da die Erdanziehungskraft einen angeblich immer zum Erdmittelpunkt ziehe, immer nur entlang eines "Großkreises" schauen müsse, könne oder solle. Eventuell ist aber jemandem von Euch aufgefallen, dass ich hier NICHT über das Kugelerde-Unfug-Modell schreibe, sondern bewusst provoziere in der Hoffnung, dass mal jemand WIRKLICH nach-denkt (anstatt längst bekannte Modelle einfach nur wiederzukäuen und in ihrer angeblichen Absolutheit und Unantastbarkeit immer wieder mental zu bestätigen) oder, besser, eigene Forschungen anstellt. Mehr sage ich dazu jetzt nicht ;-). SELBER DENKEN ist gefragt. Nur so viel: Wer mich DESHALB anschreibt und glaubt, über diesen Punkt mit mir diskutieren zu wollen, dessen email-Adresse wird SOFORT gesperrt.

Um nun abzuschätzen, was es bedeutet, wenn wir statt der 5 km - nehmen wir ruhig zugunsten des Kugelerde-Modells diesen Wert ;-) - mehr als 45 km weit "flach und geradeaus" sehen können, sehen wir uns nochmals SCHRITT 5 der Formel an:

SCHRITT 5: d = √h x √2r

Dies lässt sich bekanntlich auch schreiben als:

SCHRITT 7: d = √h x √2 x √r

Nun können wir in diese Formel problemlos einen Faktor einführen, der ein Vielfaches des "Erdradius" repräsentiert. Über diesen Faktor muss selbstverständlich ebenfalls die Wurzel gezogen werden, da über r die Wurzel gezogen wird. Die Wurzel aus z. B. 4r (wobei 4 unserem Faktor entspricht) lässt sich aber wiederum schreiben als √4 x √r:

SCHRITT 8: d = √h x √2 x √r x √F_6371km

wobei

F_6371km: das Vielfache oder auch einen Bruchteil des "Erdradius" angibt. Bei einem Vielfachen von "1" ändert sich selbstverständich nichts, da √1 = 1.

r: der "Erdradius" von 6.371 km ist.

Aus der Formel aus Schritt 8 lässt sich folgendes sehr einfach entnehmen: Wenn der "Erdradius" VIERMAL so groß wird, können wir nur ZWEIMAL so weit sehen.

Oder anders ausgedrückt: Wenn die Erde eine Kugel wäre und wir NEUNMAL so weit sehen können (Konstanz Bregenz = 46 km = > 9 x 5,05 km) wie wir es könnten, wenn der "Erdradius" 6.371 km betragen würde, dann müsste die Erde EINUNDACHTZIG MAL so groß sein, wie sie es angeblich - ALS KUGEL - ist.

Auf so einer Erde würde ich gerne leben. Denn auf dieser Erde wäre für ALLE wesentlich mehr als genug Platz vorhanden und es hätte bis heute vermutlich keinen einzigen Krieg geben müssen...

Wir sehen hier auch die leider unauflösbare Bredouille des Kugelmodells: die ENTFERNUNGEN in und zwischen einzelnen Ländern sind längst - seit Hunderten bis Tausenden von Jahren - bekannt und nicht mehr veränderlich; jedenfalls nicht wesentlich. Also KANN die angebliche Erdkugel nicht größer sein als von ihr behauptet wird. Da sie aber nicht größer sein kann, ist die einzige verbleibende Schlussfolgerung aus den hier dargestellten Beobachtungen, dass es sich bei der Erde nicht um eine Kugel handelt, sie also wohl flach sein muss. Die Theorie der Kugelerde widersteht NICHT selbst der einfachsten Falsifizierung nach Karl Popper. Punkt.

 

Update IV: Schon wieder was gelernt ;-): TERRESTRISCHE Refraktion. Wurde vom altehrwürdigen Carl Friedrich Gauß (vor allem berühmt als Mathematiker) untersucht und gemessen. Jetzt weiß ich auch, was jene meinten, die behaupteten, ich hätte Bregenz wegen einer "Lichtbrechung" sehen können und da das nun mal so sei, müsse die Formel (siehe Update III) falsch sein... Was sagt denn die "terrestrische Refraktion"? Über eine Entfernung von 10 km beträgt der Höhenfehler ca. 1 m!!!. Im Klartext: Objekte, die 10 km entfernt sind, wirken 1 m! höher (wenn das denn alles so stimmt...). Das wiederum bedeutet aber nichts anderes, als dass ein Objekt zunächst ÜBERHAUPT über eine gewissen Entfernung sichtbar sein muss, damit sich die terrestrische Refraktion auswirken kann (hieran hätte übrigens Carl Gauß sofort sehen können, dass die Erde wohl keine Kugel ist; er war neben seiner Profession als Mathematiker auch Astronom). Der Höhenfehler nimmt anscheinend quadratisch mit der Entfernung zu. Bei 46 km beträgt er dann demzufolge ca. 21,16 Meter. Glauben wir das einfach mal ;-). Dummerweise soll aber Bregenz mindestens 166 m "tiefer" liegen als Konstanz (dies ist übrigens auch auf einem Schild im dortigen Stadtgarten zu lesen, auf dem dann gleichzeitig behauptet wird, dass man DESHALB Bregenz von Konstanz aus niemals sehen könne). Was da 21 m im Hinblick z. B. auf die Yachten im Hafen und die Uferlinie ausmachen sollen, wird wohl für immer das Geheimnis derjenigen bleiben, die behauptet haben, die Formel müsse falsch sein, da man selbstverständlich Bregenz von Konstanz aus aufgrund einer Lichtbrechung sehen könne. Wo der Wunsch der Vater des Gedankens ist, hilft einfach sonst nichts mehr ;-). Jedenfalls hören wissenschaftliche Logik und Erkenntnis dort wohl ganz einfach auf...
Siehe auch meine eigenen Beobachtungen zur angeblichen "terrestrischen Refraktion" hier...

Angesichts der bisher vorgebrachten "Gegenargumente" bin ich sprachlos.

Wer solche Berater und Diskussionspartner hat, braucht keine Feinde mehr.

Hat jemand noch mehr ähnlich geniale Theorien?

Dann bitte her damit!

Übrigens: Falls sich jemand über die sehr hohe Zugriffszahl dieses Artikels wundert: Die ist (auch) das Resultat eines DDoS-Angriffs vom 07.07.2015, bei dem ausschließlich dieser Artikel im Sekundentakt ca. 40.000 mal aufgerufen wurde. Irgend jemandem ist dieser Artikel wohl ziemlich sauer aufgestossen. Da er dadurch auf meiner Startseite unter "Blog - Meistgelesen" wohl uneinholbar vom absolut letzten auf den ersten Platz katapulitert wurde, sage ich: HERZLICHEN DANK für diesen Angriff!
Mal als kleiner Denkanstoss an die Angreifer: Bleibt einfach locker. So gut wie immer erreicht man durch Druck das genaue Gegenteil des Beabsichtigten. Ich hätte mich ganz sicher nicht hingesetzt und so oft auf diesen Artikel geklickt, nur um ihn auf Platz 1 zu bringen...
Die über 40.000 hinaus gehenden Zugriffszahlen sind aber echte Zugriffe, worüber ich mich sehr freue...